Model-based Method: Kalman Filter

1. Fault Information

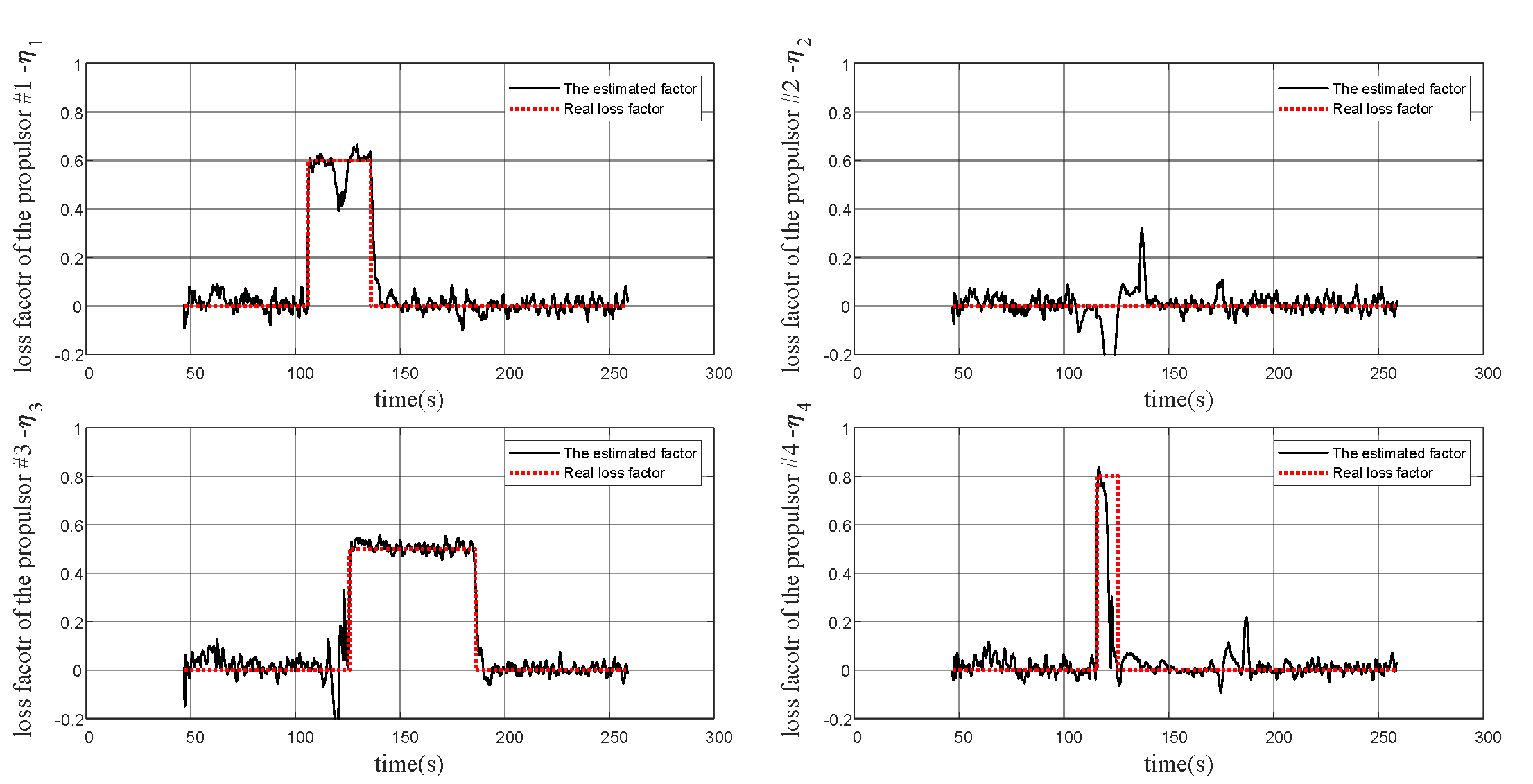
An essential application for RflyMAD is to construct fault diagnosis methods. Here we take a simple fault type as an example to diagnose. Detailed information about this fault could be seen in the following table.

Fault Type	Start Time	Duration	Fault Parameter	Flight Status
Motor(1)	106s	30s	0.6	Hover
Motor(4)	116s	5s	0.8	Hover
Motor(3)	126s	60s	0.5	Hover

$i^{th}$ motor of multicopter has a fault.

From the table, we could know that the multicopter is hovering while the faults are injected. Start time means when the fault is injected during the whole flight process. The data used in this sample is an HIL simulation data, and mainly message topics are in ULog data that can be accessed from here.

2. Simplified Dynamic Model Construction

$\eta_{i}\in[0,1],i=1,2,3,4$ $\eta_{i}$ $i^{th}$ $(1-\eta_{i})\times100\%$ $i^{th}$ $f_{i}$ , we could write loss factor and thrust in the forms of vector and matrix as

\begin{aligned} f & = [f_{1} f_{2} f_{3} f_{4}]^{T}, Γ_{f} = d i a g (f_{1}, f_{2}, f_{3}, f_{4}), \\ η & = [η_{1} η_{2} η_{3} η_{4}]^{T}, Γ_{η} = d i a g (η_{1}, η_{2}, η_{3}, η_{4}) . \end{aligned}

In order to detect the fault by using the RflyMAD dataset, we need to find the relationship between the loss factor and the states of quadrotors. Considering the multicopter is hovering when the faults occur, we could neglect aerodynamic damping and make a small angle assumption to build a simplified function to describe the movement of the quadrotor as ¹ ²

\begin{aligned} \ddot{z} & = \frac{T}{m} - g \\ J_{x} \ddot{ϕ} & = τ_{x} \\ J_{y} \ddot{θ} & = τ_{y} \\ J_{z} \ddot{ψ} & = τ_{z} \end{aligned}

$(x, y, z)$ $(\phi, \theta, \psi)$ $(J_x, J_y, J_z)$ $T$ $(\tau_x, \tau_y, \tau_z)$ $m$ is the mass of the quadrotor. So the linear approximate state equation of the quadrotor aircraft system at low speed and small angle is

\dot{x} = Ax + B \underset{u}{\underset{⏟}{(u_{f} - g)}} = Ax + B (B_{f} f - g)

$\mathbf{B}_f \in \mathbb{R}^{4\times4}$ is the control efficiency matrix ³, specific expressions of the state vector and other parameters are

\begin{aligned} x & = [z ϕ θ ψ \dot{z} \dot{ϕ} \dot{θ} \dot{ψ}]^{T} \in R^{8}, \\ u_{f} & = [T τ_{x} τ_{y} τ_{z}]^{T} \in R^{4}, \\ g & = [m g 0 0 0]^{T} \in R^{4}, \\ A & = [\begin{array}{c} 0_{4 \times 4} & I_{4} \\ 0_{4 \times 4} & 0_{4 \times 4} \end{array}] \in R^{8 \times 8}, \\ B & = [\begin{array}{c} 0_{4 \times 4} \\ J_{f}^{- 1} \end{array}] \in R^{8 \times 4}, \\ J_{f} & = d i a g (- m, J_{x}, J_{y}, J_{z}) \in R^{4 \times 4} . \end{aligned}

Taking the loss factor into consideration, we could change the control input like

\begin{aligned} u & = B_{f} (I - Γ_{η}) f - g \\ = B_{f} f - g - B_{f} Γ_{η} f \\ = u_{0} - B_{f} Γ_{f} η \end{aligned}

$\mathbf{\eta}$ $\tilde{\mathbf{x}}$ and discretize the state function. We could get the final function used for state estimation as

\begin{aligned} {\dot{\tilde{x}}}_{k + 1} & = [\begin{array}{c} I_{4} & I_{4} Δ t & - \frac{Δ t^{2}}{2} M \\ 0_{4 \times 4} & I_{4} & - Δ t M \\ 0_{4 \times 4} & 0_{4 \times 4} & I_{4} \end{array}] {\tilde{x}}_{k} + [\begin{array}{c} \frac{Δ t^{2}}{2} J_{f}^{- 1} \\ Δ t J_{f}^{- 1} \\ 0_{4 \times 4} \end{array}] u_{0}, \\ y & = [I_{8 \times 8} 0_{8 \times 4}] {\tilde{x}}_{k}, M = J_{f}^{- 1} B_{f} Γ_{f} \end{aligned}

$\Delta t$ $\tilde{\mathbf{x}}$ $(x, y, z)$ $(\phi, \theta, \psi)$ $(\dot{\phi}, \dot{\theta}, \dot{\psi})$ $\sigma$ of multicopter is in need. In our RflyMAD dataset, it could be get from the ULog data by using the toolkit we developed and introduced in Dataset. The detailed information about the data in shown in the following table.

Symbol	Source File in ULog	Usage
$\sigma$	actuator_outputs_0.csv	Input parameter of ESC
$(x, y, z)$	vehicle_local_position_0.csv	Observation vector of KF
$(\phi, \theta, \psi)$	vehicle_attitude_0.csv	Observation vector of KF
$(\dot{\phi}, \dot{\theta}, \dot{\psi})$	sensor_combined_0.csv	Observation vector of KF

Note: Other information like physical parameters of the multicopter is shown in OpenHA-Models or documents in our RflyMAD dataset.

3. Experimental results

With the Kalman Filter and detailed information from RflyMAD dataset, the estimated results are shown in the following figure. Compared with the actual fault information, we could find that the estimation result is accurate.

The above steps show how to use RflyMAD dataset in the process of fault diagnosis, and users can apply their own methods with more message topics in our RflyMAD dataset to get a better results!

1 Xu, R., & Ozguner, U. (2006, December). Sliding mode control of a quadrotor helicopter. In Proceedings of the 45th IEEE Conference on Decision and Control (pp. 4957-4962). IEEE. ↩

2 Amoozgar, M. H., Chamseddine, A., & Zhang, Y. (2013). Experimental test of a two-stage Kalman filter for actuator fault detection and diagnosis of an unmanned quadrotor helicopter. Journal of Intelligent & Robotic Systems, 70, 107-117. ↩

3 Du, G. X., & Sun, L. (2018, July). Loss of effectiveness information observability analysis for multicopters. In 2018 3rd International Conference on Advanced Robotics and Mechatronics (ICARM) (pp. 572-576). IEEE. ↩